Use our negative numbers worksheets and the advice below to tackle this particular area of mathematics with your KS2 pupils…
Negative numbers worksheet

Our negative numbers worksheet will give your KS2 pupils plenty of negative number practice. Pupils will practise:
- Counting backwards through zero including negative numbers
- Solving number and practical problems that involve negative numbers
- Interpreting negative numbers in context
- Counting forwards and backwards with positive and negative whole numbers including through zero
- Counting backwards through zero including negative numbers
Download this negative numbers worksheet from the top of this page.
This download also contains three sets of negative number worksheets from White Rose Maths, covering counting backwards and forwards in negative numbers to problem-solving with negative numbers.

What are negative numbers?
Negative numbers are a type of numerical value that represent quantities less than zero. They are essentially the opposite or inverse of positive numbers.
Teaching negative numbers is crucial as it enables understanding of real-world situations like temperatures below zero and financial transactions. It also develops mathematical skills for operations, algebraic reasoning, and problem-solving.
Where are negative numbers taught in the primary curriculum?
The primary national curriculum introduces the concept of negative numbers in Year 4 where the children learn to count backwards through zero and into negative numbers.
Statutory national curriculum objectives
- Count backwards through zero including negative numbers (Year 4)
- Interpret negative numbers in context, count forwards and backwards with positive and negative whole numbers including through zero (Year 5)
- Use negative numbers in context, and count intervals across zero (Year 6)
- Solving number and practical problems that involve negative numbers (Year 6)
Non-statutory guidelines (Year 6)
- Using the number line, pupils use, add and subtract positive and negative integers for measures such as temperature.
- Pupils draw and label a pair of axes in all four quadrants with equal scaling. This extends their knowledge of one quadrant to all four quadrants, including the use of negative numbers.
Initial things to think about
Introducing children to numbers below zero opens up a new world to them. The idea that numbers can be less than zero introduces a totally new way of thinking about maths.
One of the challenging things to get children to remember is that when we use negative numbers, the larger the digit the smaller the number.
Naturally, because they’ve had seven or eight years of experience of learning about numbers gaining value as the digits get bigger, children often initially see larger digits as being a bigger number even when the negative context is introduced.
“The idea that numbers can be less than zero introduces a totally new way of thinking about maths”
This is where using ‘zero’ and a number line is very helpful. Teaching children on a number line and recognising that when numbers get further away from the zero (on the negative side) the smaller the number is, should be one of the first things to think about when we address the Year 4 objective to ‘count back through zero including negative numbers’.
Another new concept for the children is recognising the negative symbol (-) to represent negative numbers and not just when used for subtraction.
This is where mathematical language is especially important, as the children should begin to use the word ‘negative’ when using the – symbol in this context. It is therefore important that you continue to model that language in class (-5 is ‘negative 5’ for example).
Introducing negative numbers using a number line
Using a number line when teaching negative numbers is a helpful visual tool that aids in understanding and conceptualizing the concept. It helps with:
- Visual representation: A number line provides a clear visual representation of numerical order, including positive and negative numbers. It allows students to see the relationship between numbers.
- Sequential order: It helps students understand that numbers are arranged in a specific order. They can see that as they move from left to right, the numbers increase, and as they move from right to left, the numbers decrease.
- Relating numbers: The number line helps students understand the relationship between different numbers. They can easily see that numbers to the right of zero (positive numbers) are greater than zero, while numbers to the left of zero (negative numbers) are less than zero.
- Adding and subtracting: The number line is useful for teaching addition and subtraction of negative numbers. Students can physically move along the number line to understand the effect of adding or subtracting a specific value.
- Real-world examples: By using a number line, teachers can provide real-world examples that students can relate to, such as temperatures, bank balances, and elevations. This helps students connect the abstract concept of negative numbers to practical scenarios.
Common early misconceptions
Adding a negative number makes the value smaller
Children may struggle to understand the concept of adding negative numbers. Some pupils may mistakenly believe that any calculation involving a negative number always results in a smaller value.
However, it’s crucial to clarify that it depends which way round we do it.
For example, if we start with a negative number and add a positive number, the answer is larger than the original negative value: -4 + 3 = -1. (Negative one is larger than negative four.)
But, if we start with a positive number, and add a negative number, the answer is smaller than the original positive value: 4 + -3 = 1. (One is smaller than four.)
Activity example
To begin with, start on the ‘right’ side of the number line (on the positive side) and carry out a number of calculations where you start with a positive number and add a negative number. Don’t cross through zero yet as this can be done once the children are more confident.
The children will spot a pattern that each time a negative number is added to a positive number, the answer gets smaller. They will assume that when adding a positive number and negative number together you will always get a smaller answer.
You can then ‘test’ this by starting on the ‘left’ side of zero (the negative side) and take a negative number and add a positive number to it. They will quickly notice that this way round the answer actually gets bigger.
Once the children are confident in recognising negative numbers and using number lines to cross through zero, etc, they can move on to adding and subtracting negative numbers with whole numbers.
Again, this is where it is important to think about the number line and explain how when negative numbers have a whole number added to them, the answer moves closer to (and through if required) the zero.
Do not underestimate how important the number line element of negative numbers is! Spend plenty of time getting the children confident this way first.
“Do not underestimate how important the number line element of negative numbers is”
Negative numbers don’t exist in real life
Pupils may find it difficult to relate negative numbers to real-life situations. They might think that negative quantities or temperatures, for example, are impossible or have no practical significance.
It can be helpful to provide examples such as temperatures below zero, or the concept of debt, to demonstrate real-life applications of negative numbers. Contextualising negative numbers is important to add more meaning and use to learning.
Activity example
To address these misconceptions, we should be using concrete examples, visual representations and real-world applications to help students develop a solid understanding of negative numbers.
By providing multiple opportunities for hands-on practice and meaningful discussions, we can help students overcome these misconceptions and build a strong foundation in mathematics.
You can do this via simple examples such as showing your class:
- Temperature charts (of different places during winter, for example) and comparing real-life negative numbers.
- How money can actually go below zero when talking about ‘debt’.
- Examples of thermometers reading less than zero.
Real-world applications are what really allow children to move forward with their understanding of negative numbers and shows them how ‘real’ these numbers are.
It allows us to bring negative numbers into real life rather than just seeing them as patterns on a number line, or figures we add or subtract.
“Real-world applications are what really allow children to move forward with their understanding of negative numbers”
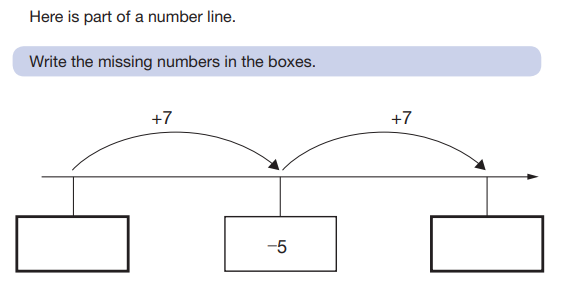
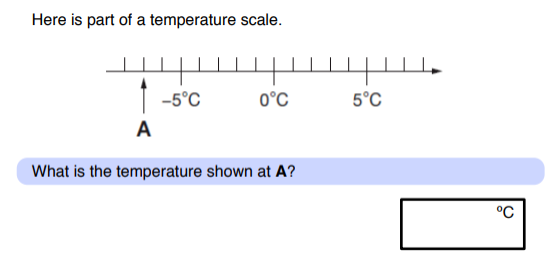
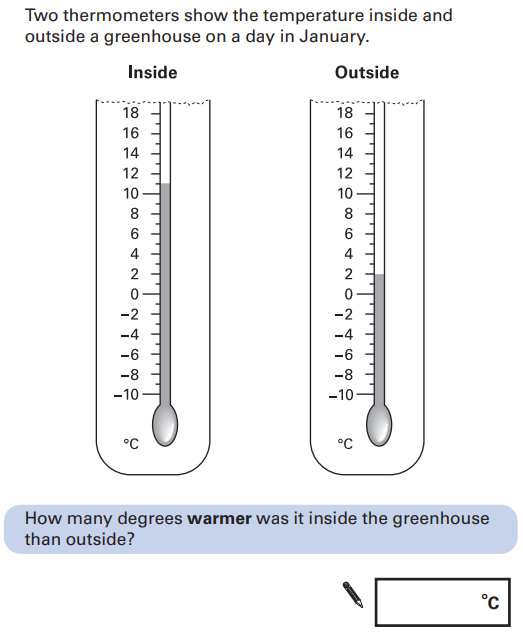
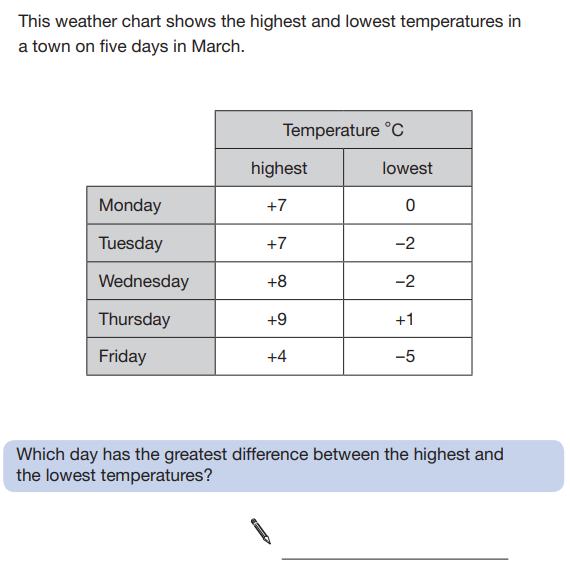
Examples of negative number SATs questions
These eight questions have all been taken from previous papers.




James Grocott is a Year 4 teacher, maths lead, and deputy head in Suffolk.