Task sheet and table showing bearing of each letter from every other letter
KS4
Years 10-11
In this bearings maths lesson, students will make up and decode cryptic messages using bearings. Each word is coded as a journey from one letter to the next on a spiral grid of letters.
Bearings are a precise way to describe one location relative to another, and have widespread uses. They can be a useful context for working with angles.
Students will need to be precise about their angles and distances, or they will not be able to code or decode the message successfully! This task provides plentiful opportunities for students to develop fluency with interpreting and using bearings, and may also enable them to notice connections between bearings and back-bearings.
Bearings maths starter activity
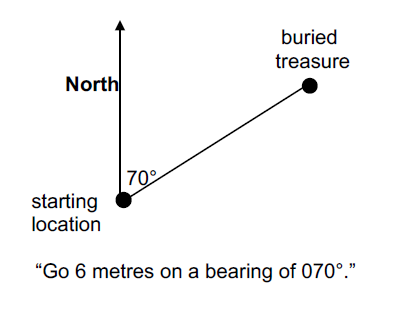
Q. Imagine you have buried some treasure underground and you want to tell someone else exactly where the treasure is. How could you do that?
Students may suggest taking the person there and showing them the spot, or drawing them an accurate map. But ask students to imagine that that is not possible – perhaps they are a long distance away and can only explain by speaking over the phone.
Students may suggest instructions such as “Go 3 metres this way and 4 metres that way”, etc., but it can be hard to specify the exact directions to go in. If no one suggests using bearings, suggest it by showing how a distance and an angle (relative to some direction, such as North) are needed.
Key question
How can we tell someone exactly which direction we want them to walk in?
Main activity
Remind students of three rules for using bearings. We always:
- Measure from the North direction
- Measure clockwise
- Give 3 digits (so 70°, for example, is 070°)
To send someone to an exact spot, we have to tell them two things.
- The bearing
- How far to go (the distance) in that direction
Q. Why do we need both of these?
The bearing alone indicates only a direction – the desired point could be anywhere along that (half) line.
The distance alone indicates somewhere on a circle centred at the starting point, but the desired point could be anywhere around the circumference of that circle.
Give students a sheet showing the spiral alphabet, which looks like this (included in the resource downloads for this maths lesson plan, just hit the ‘Click to download PDF’ link at the top of the page):
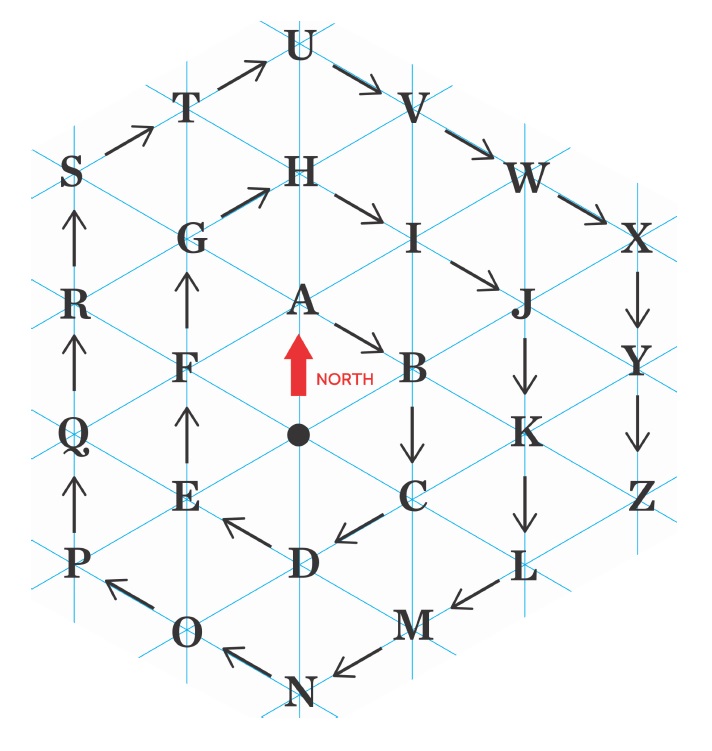
Coded messages
Q. In this lesson we are going to make up some coded messages for each other using bearings. On this grid are all the letters of the alphabet. Imagine we wanted to send the message ‘CODE’. We start at the dot in the middle of the drawing. The first letter is C, so we need to give the bearing and distance to the letter C.
Students can measure the distance with a ruler, and should get 3cm.
Q. What is the bearing from the dot to C?
Students will need angle measurers and may need help with this. They may say 060°, because they focus on the 60° angles in the triangles. They may go anticlockwise and say 300°. The correct answer is 120°. So the instruction would be: “Go 3cm on a bearing of 120°.”
Q. Now we are at C and we need to get to the next letter, which is O. What instruction do we need?
Complete this code as a whole class, obtaining:
C – Go 3cm on a bearing of 120°.
O – Go 6cm on a bearing of 240°
D – Go 3cm on a bearing of 060°
E – Go 3cm on a bearing of 300°
[Students may find ‘D’ hard, because it is a “back bearing” of the previous one – and they may forget to include 3 digits, as well.]
Q. Now your task is to make up your own code for someone else. Remember that I know the code, so make sure that your messages are ones you would be happy for me to read! Start with a short message. Don’t worry about punctuation or spaces – the decoder can work that out by themselves.
Give students time to create some coded messages. You could tell them that they have 5 minutes to create their first message, and then after 5 minutes everyone swaps with someone else to decode.
Some students will manage longer messages than others in this time. You may need to say that it is OK to jump across the grid; for example, from E to W or M to U.
Discussion
You could conclude the lesson by talking about the codes that students have made and solved and which messages were trickiest and why.
Q. Which messages were easy and which were hard? Why? Did you make any mistakes when coding or decoding? Where did you slip up? What are the easy ways to go wrong with bearings? What helps to get it right?
When coding, some students may have chosen their messages so that they involved letters close to each other on the grid. Some may have chosen to move in a North-Easterly direction, so as to avoid reflex angles, and this could be useful to talk about. When decoding, however, they will not have been able to control this!
Additional bearings maths resources
- A table, for the teacher’s benefit, showing the bearing of each letter from every other letter, is available as part of the PDF resources download (link at top of article)
- A nice task involving bearings is available at nrich.maths.org/6263
Key resource
Practising Mathematics – Developing the Mathematician as well as the Mathematics (by Tom Francome and Dave Hewitt).
This new book from the Association of Teachers of Mathematics is full of ideas, tasks and activities for practising the content of the secondary mathematics curriculum. It aims to develop pupils reasoning and problem solving skills that are so vital for success in school and beyond. The book covers numerous areas of the mathematics curriculum, including Number Work, Ratio and Proportion, Algebra, Geometry, Probability and Statistics and is accompanied by a set of resource cards. Buy it here.
Colin Foster is an Assistant Professor in mathematics education in the School of Education at the University of Nottingham. He has written many books and articles for mathematics teachers (see foster77.co.uk).














