Teaching Simplification of Algebra so Kids Actually Understand

If your students are making mistakes with collecting like terms in algebra, it could be because they still don’t fully understand addition, says Peter Mattock…

- by Peter Mattock
- Assistant headteacher, maths SCITT lead, SLE and author Visit website

Talk to any secondary maths teacher across the country who has been in schools at least a couple of years, and they will recognise the scene; reviewing some book work or an assessment, and student after student has written:
3x + 2y + 4x + 3y = 7x + 5y = 12xy
Of course, the first line is right, but the second line doesn’t follow. It is something that kids make up because they just can’t stand the thought of leaving a final answer that still has a plus sign in.
Fundamentally, this comes from a lack of understanding of both addition and the point of algebra. Algebra captures those things that are generalisable – in this case, that are true no matter what the values of x and y.
It is true that 4 lots of any number plus 3 lots of the same number will always give 7 lots of that number (3x + 4x = 7x), and similarly with 2 of any number and 3 of that number (2y + 3y = 5y).
But it isn’t true that 7 of one number + 5 of a different number always gives 12 of the product of the two numbers.
It may be true for certain numbers (in this case when x and y both equal 1 or 0), but not all values of x and y.
Adding up
How can we correct this misunderstanding? Or even better, how can we stop it forming in the first place?
To start with, we need to make sure pupils understand addition fully; not just 3 + 4 = 7, but also 3 × 11 + 4 × 11 = 7 × 11, 3 × 1.1 + 4 × 1.1 = 7 × 1.1 and 3/11 + 4/11 = 7/11.
To completely understand this, pupils also need to see non-examples.
So, whilst 3 × 11 + 4 × 11 = 7 × 11, 3 × 11 + 4 × 13 cannot be evaluated until 3 × 11 and 4 × 13 are separately calculated.
Using manipulatives and intelligently designed questions/activities can support with this.
Then, when we are ready to generalise this to addition and subtraction with algebra, we can use the same manipulatives and intelligently designed activities to reinforce the links between the algebra and what we already know from numbers.
One way of doing this is through using algebra discs to support the addition and subtraction of algebraic terms.
The idea behind algebra discs is to allow each variable to be treated like a collection of objects. This is analogous to how we might treat a value when modelling a calculation.
For example, if modelling the calculation 3 × 11 + 4 × 11, and aiming to show why the result is 7 × 11, we might use counters with a ‘worth’ of 11, ie:
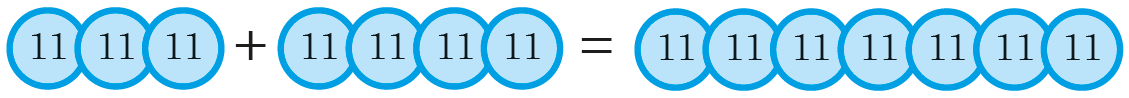
Similarly, algebra discs use different coloured counters for each variable, as well as the negative of the variable, and also the squares and negative squares of each variable.
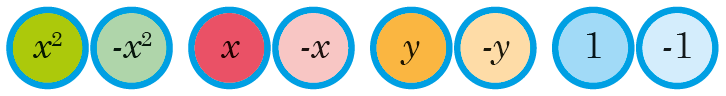
Like what?
One thing that teachers can neglect when beginning to apply knowledge of addition and subtraction to algebraic terms is recognising when two or more terms are talking about the same ‘number’, ie are like terms.
This is why the non-examples when working on addition are so important, as this gives pupils a background in seeing that when part of each product is the same (3 × 11 and 4 × 11) they can be added, but when no part of each product is the same (3 × 11 and 4 × 13) the same is not true.
Trending
It is also a good idea to revisit this with algebraic notation before actually looking at adding and subtracting like terms.
Tackling all the common misconceptions ahead of time is important, such as different exponents of x, as well as including some less seen examples (non-standard examples) such as terms with fractional and negative coefficients.
Time also needs to be made to assess pupil understanding of this before introducing addition and subtraction of terms, using short but intelligently designed questions, and a whole-class method of response, like mini whiteboards, voting software or even ‘thumbs up, thumbs down’.
More examples
When modelling, or asking pupils to explore the different expressions, a limited scope of examples can lead to the problem of under-generalisation, where pupils only apply what they have learnt to the limited example set for which they have seen it used, or used it themselves. Routinely missed out are:
- Terms with variables as products (eg 4xy + 2xy)
- Terms with fractional or decimal coefficients
- Expressions with more than 4 terms added/subtracted
- Terms where many of the variables won’t simplify (eg 2x2 + 3x – 5 + 2x)
Constant terms are another ofttimes a glaring omission. Pupils learn to simplify 3x + 2y + 5x + 4y, but then fall down when asked to simplify 3x + 2 + 5x + 4.
The lack of variable attached to the 2 and the 4 can throw pupils off unless they face it early on and work with it in a concrete way.
Smart tasks
When it comes to working independently, the choice of task is crucial.
Mechanical repetition of the skill of simplification over and over again may drill a process into a pupil’s head, but it is likely to become a relatively ‘mindless task’, to be completed with little attention.
A better approach is to use a task that can prompt thinking.
This could be a series of questions that are very closely related, so that pupils have to attend more to the differences between them and, naturally, between the answers, too.
Alternatively, it could be a more open activity where pupils are creating expressions that meet certain criteria. Examples of both are given below:
1 | Minimally different questions
- 8x + 8y + 5x + 5y
- 8x +8y – 5x – 5y
- 8x – 8y + 5x – 5y
- 8x – 8y – 5x – 5y
- 8x – 8y – 5x + 5y
- 5x + 5y – 8x + 5y
- 5x – 5y – 8x – 8y – 5x – 5y – 8x – 8y
- 8x – 5y – 8x + 5y
- 8x + -5y + -8x + -5y
- 8x – -5y – -8x – -5y
- 8x – 5y + 3z – 8x + 5y + 4z
- 8x – 5y + 3x2 – 8x + 5y + 4x2
2 | An open activity of creating different expressions:
Find as many expressions as you can that simplify to give: 7x – 2y + 3. Bonus points if you can find an expression where letters other than x and y are also used.
Finally, whilst assessment throughout the lesson is important so adjustments can be made as needed, I also like to check at the end of a lesson for anything I may have missed to inform my future planning.
Whilst no quiz or activity conducted at this point can tell you if pupils have learned what you wanted them to (because they haven’t even had chance to forget it yet!), it will let you know if there is an early issue of misunderstanding.
The use of manipulatives and imagery, blended with carefully thought out example and question sets, intelligently designed to highlight important ideas, is a much more effective approach to teaching what can be pupils’ first foray into the world of manipulating algebra than many others I have seen in the classroom in my years of experience.
And it is important we get this right and allow pupils to feel successful with it – because every maths teacher knows pupils whose early experiences of algebra are bad ones, producing negative associations that can take years to untangle.
Peter Mattock is a head of maths and secondary mastery lead for the East Midlands South Maths Hub. His book, Visible Maths, was published in February (Crown House, £18.99). Follow him on Twitter at @MrMattock.










