Use primary maths resources from NCETM and White Rose Maths to improve your maths planning

Beth Smith explains how new advice from the DfE and NCETM can help you to focus on key learning in maths and support children to build strong foundations…

- by Beth Smith

For the past few years I’ve had the pleasure of working with trainee teachers, delivering maths content on a School Direct programme.
In addition, this year I’m working with NQTs and RQTs to support their teaching in all areas, including maths. This work has led me to deeply consider how to support new teachers to plan maths effectively.
There is now an abundance of maths resources available and I’ve seen first-hand how this can cause teachers to feel overwhelmed and spend their planning time navigating websites for activities for the children to do.
Rather than planning what children are going to do in maths, we need to consider what pupils are going to learn.
This shift in thought is key, especially for new teachers. We can sometimes spend our planning time collating questions and activities for children to do, without spending enough time thinking about how this links to what pupils are learning.
Even if you’re using an effective set of questions, the way you deliver the lesson and structure the learning is the key component to children’s understanding of maths.
What follows are some key aspects that you should consider when planning maths lessons, regardless of the resources you’re using.
There are also special considerations to be made this year, related to teaching in a more socially distanced manner.
Starting points
The first key consideration is children’s starting points.
With disruption to learning, we need to give even more consideration to previous years’ learning.
White Rose Maths has added recap steps to this year’s curriculum to allow you time to recap previous content.
It has also produced a Y1-6 progression document to support a teacher’s overview of progression through the curriculum.
The National Centre for Excellence in the Teaching of Mathematics (NCETM) has a brilliant national curriculum tool on its website that allows you to look at blocks of learning and consider what has come before and after.
You can also look at suggestions for activities and find articles, videos and exemplifications of learning for your year group.
Another key document is the Ready to Progress criteria, released by the DfE and NCETM in June.
As part of its aim to “summarise the most important knowledge and understanding within each year group and important connections between these mathematical topics”, the document highlights key learning for each year group. Interestingly, this document was already planned before the disruption to last year’s learning had even happened.
It links well with NCETM’s professional development materials, which bring a coherence to thinking in primary maths and will help you to consider key representations and language to support children to develop their understanding of the structure of maths.
Socially distanced CPA
Representations are the next key aspect that you need to consider when planning.
The shift towards concrete and pictorial representations in the past few years has been fantastic and has truly helped children to develop conceptual understanding.
However, as we now consider teaching in the middle of a pandemic, I’ve witnessed teachers struggling to use concrete representations in a classroom where equipment cannot be shared as freely.
Although it won’t be easy, it is vital that children continue to have hands-on experiences in order to develop understanding.
There are many online tools, animated PowerPoints and interactive slides that can model this learning to pupils, although these don’t fully replicate the experience of using actual equipment.
When planning, think carefully about the key models that children need to use.
Use counters or buttons on a place value grid, use squared paper to make Base 10 ones, tens and hundreds, or create ten frames out of egg boxes.
Instead of just looking at images of concrete representations on worksheets or PowerPoint slides, it’s vital that children actually use them if they are going to truly understand concepts deeply.
Consistent language
Linked to representation is language. The Ready to Progress criteria features ‘language focus’ sections throughout.
Ensure your maths language is consistent across your school. A noticeable use of language is in Y1, where the document suggests the following:
Language focus
“…seven, eight, nine, ten, eleven, twelve, thirteen… twenty, twenty-one, twenty-two…”
“…seven, eight, nine, one-ten, one-ten-one, one-ten-two, one-ten-three… two-tens, two-tens-one, two-tens-two…”
This use of language supports children to understand the structure of numbers.
If you only use the national curriculum objectives to plan, you won’t see this language in use.
I’ve worked with Y1 teachers in the past who have been reluctant to introduce this language as it wasn’t in the statutory guidance, even though it’s vital for helping children to understand how numbers are built, rather than just learning a number name.
It’s also key to consider consistency of language throughout year groups and topics.
The language we use allows children to make connections between mathematical ideas.
As in the NCETM materials, White Rose Maths materials also develop this effective language throughout its schemes to support children’s understanding.
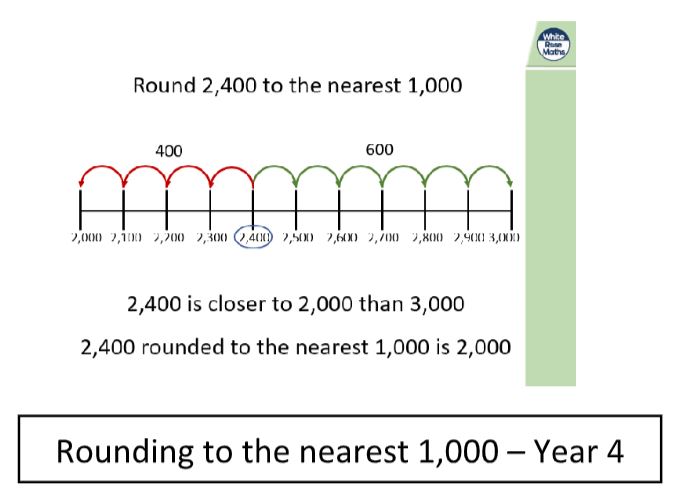
Take the use of number lines and rounding, for example. Here are two examples from the Y4 programme:
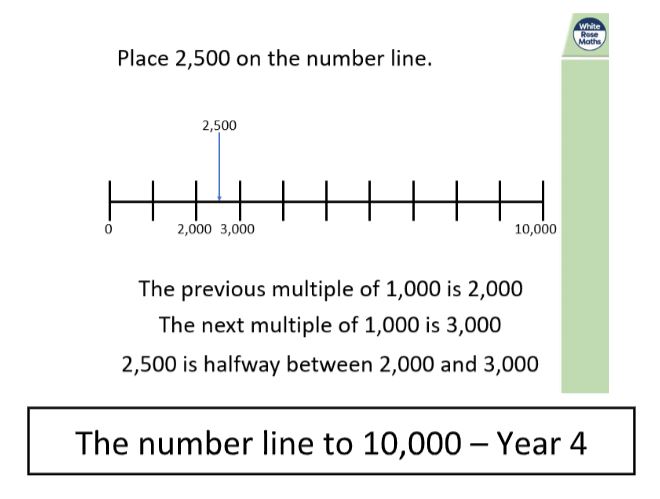
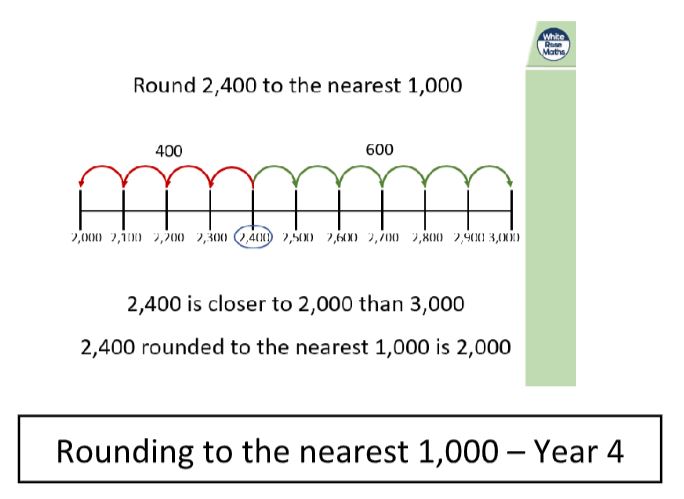
Here, the key language of ‘previous multiple’ and ‘next multiple’ is re-considered in the context of rounding and how close the number is to the multiples.
This language is consistent with that in the Ready to Progress criteria, supporting teachers to use the language consistently throughout school.
Making generalisations
Drawing representations and language together, the final aspect we need to consider is how we can plan to focus children’s learning through the use of generalisations.
The second aim of the national curriculum is to “reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language.”
There has been a big shift in focus towards reasoning since the 2014 curriculum, with teachers asking children to explain their thinking more in both verbal and written ways.
However, this is still an area that some teachers can struggle with when planning how this is developed in lessons.
In the same way that we teach children procedures and methods, we also need to consider how we develop their reasoning.
One way to do this is to focus on making generalisations. Take a look at this White Rose Maths Y4 image for adding and subtracting ones, tens, hundreds and thousands.
Here, the language ‘always’, ‘sometimes’ and ‘never’ is used to create generalisations.
Using place value counters, children can add hundreds and consider which columns are affected.
After completing a few examples, they can draw conclusions under each column.
Consider how this language can then be applied to adding and subtracting different powers of ten. The generalisation here leads us to see that the column we are adding is always changed (unless adding ‘0’).
The columns to the right never change, and the columns to the left sometimes change.
But why is this generalisation so important?
When children add using the column method, a common misconception is to add from left to right.
When reflecting on why this is incorrect, this image explains that we must add right to left because adding can affect the columns to the left.
Once we’ve added, the columns to the right are no longer affected.
The same applies with subtraction so you can apply the generalisation later in the learning sequence.
It’s about making connections and strengthening understanding so that maths becomes interconnected and children can see how key ideas can be built upon.
Key learning
These are some key ideas to think about when you consider your maths planning.
The latest guidance from the DfE and NCETM, along with other effective resources, can provide you with support to ensure that representations and language are consistent throughout children’s learning.
Always remember to focus on what the key learning is, and support children in making generalisations which can be referred back to as they build on their strong mathematical foundations.
Beth Smith is a primary maths specialist for White Rose Math. Find her on Twitter at @beth_89.







