Language-Based Maths Activities Should be the Vital 4th Component of the C-P-A Approach

“Ensuring that language is purposefully intertwined with our teaching approach strengthens the learning process”

Many years ago, as a young primary school teacher, I wondered why, on occasion, I was met with a sea of blank faces when asking children to recall a maths lesson from last week or even just the day before. This interested and perplexed me in equal measure as I (somewhat naively) believed that I taught maths well and therefore it followed that the children learnt maths well.
Although I used concrete resources, jottings and different methods of recording, I did not regularly and consistently follow the Concrete-Pictorial-Abstract (C-P-A) approach, first proposed by Jerome Bruner in 1966. Through his research on the cognitive development of children, Bruner outlined three modes of representation, which have historically been viewed as developmental in order:
- Enactive representation (action-based)
- Iconic representation (image-based)
- Symbolic representation (language-based)
I understood that the C-P-A approach supported mathematical understanding (and learning wholesale) and I did, as a consequence, plan for investigative work where children manipulated resources to support their exploration of pattern, mathematical problems or new ideas.
But, on reflection, I did not have enough volume, or indeed variety, of manipulatives to utilise them to their full potential and, subsequently, did not use such resources regularly enough to make an impact.
Neither did I, like many teachers I guess, recognise the importance of the pictorial phase and therefore did not utilise such representations (pictures, drawings and two-dimensional representations of mathematical ideas) frequently enough; often moving from action-based learning to abstract recording too quickly, without fully appreciating that even the written form of a number idea (a numeral such as ‘5’) is an abstract representation.
Applying the C-P-A approach consistently – always teaching a new mathematical idea using concrete representations and utilising pictorial and abstract ways of working as understanding develops – is crucial for tackling new ideas and gaining understanding. However, this is not the only consideration when trying to avoid a classful of children with glazed eyes.
In order to remember in a flexible and adaptable way that enables children to apply what they know to new situations, the transfer of learning from the ‘here and now’ to long term memory needs to happen – and this does not necessarily follow purely because the C-P-A approach has been employed. Children need to conjecture, reason and justify.
Bruner described the symbolic stage as language based. Reasoning requires language and can be thought of as comprehension in mathematics, as it is really about sense making.
Ensuring that language is purposefully intertwined with our teaching approach strengthens the learning process and, as such, further develops understanding of the mathematical ideas being explored.
Consequently, when designing maths lessons, teachers need to think about this carefully and plan to scaffold the reasoning and language opportunities more precisely. This is known as the ‘connected model of learning mathematics’, skilfully represented in this diagram by Haylock and Cockburn.
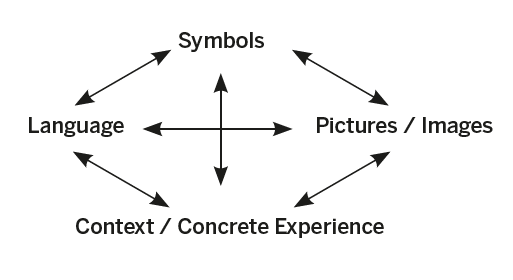
This model firmly places language-based activity, eg the utilisation of discussion, mathematical vocabulary, thinking, problem solving and reasoning, on an equal footing with concrete, pictorial and abstract representations. It also reaffirms my belief that the C-P-A approach does not need to be followed in a linear fashion from C through to A but can – and should! – be fluidly applied, linking the four key elements in a more ‘interconnected’ manner.
While this model supports successful learning, there are still barriers to overcome on the journey from first meeting a mathematical idea to understanding it and then committing it to an appropriate memory bank where it can be accessed again and applied in new and flexible ways.
Trending
In order for this transfer to be successful, new learning needs to be presented in an understandable way, but one that also challenges children to think hard about what they are learning (if they think hard, learning is more likely to pass from a child’s short-term memory to their long-term memory).
The aim of a lesson should be for children to think about meaning – which brings us back to comprehension, and comprehension of a mathematical idea does not need to be delivered in a novel and exciting way to be remembered.
In fact, if we make something too exciting, we might risk children remembering the sensory experience they had (episodic memory) rather than the concept or procedure that was being taught (semantic memory). As teachers, we have to be mindful of this fact, as it is a semantic memory that children need for future use and application, an idea put forward by psychology professor Daniel Willingham.
Importantly, I have also come to understand that children need to forget; it is part of the learning process. Rather than feeling frustrated that they just haven’t learnt what it was that we were teaching, we must feel spurred on to revisit and reactivate the temporarily ‘lost’ knowledge.
Children will remember quicker and learn more on the second and third visit to a mathematical idea, because we are strengthening the memory each time we revisit, meaning that children retain more, and for longer. Thus the process of remembering and recalling becomes more automatic.
This is known as ‘spaced repetition’ and is seen by some as a highly effective way to learn and remember, since it utilises the brain’s systems most effectively.
If we buy in to this notion, it follows that schools need to design their curriculum to allow for revisiting what has been taught in the previous week, half term, term and year to support the transfer of knowledge to long-term memory.
This is definitely something to be mindful of at this time of year, when your new class seems to have forgotten everything that their previous teacher said they had secured. It will come back, just take a deep breath…
Delve deeper
- Toward a Theory of Instruction by Jerome Bruner (£22.95, Harvard University Press)
- What Every Teacher Needs to Know About Psychology by David Didau and Nick Rose (£18, John Catt Educational)
- Understanding Mathematics for Young Children by Derek Haylock and Anne D Cockburn (£24.99, Sage Publications)
- Why Don’t Students Like School? by Daniel Willingham (£15.99, Jossey Bass)
Louise Pennington is professional development leader for maths and Numicon at Oxford University Press. Explore Louise’s video tutorials and hints for using manipulatives here. You can also follow her on Twitter at @pdlouisep.