KS3/4 Maths – Why practical work is more useful than you think

If the engagement levels of your maths lessons are lower than you’d like, technology-based practical work can do much to ignite pupils’ imaginations, suggest Keith Parramore and Joan Stephens…

Back in 1982, paragraph 243 of ‘Mathematics Counts’, AKA The Cockcroft Report, listed six elements for which opportunities should be found in the mathematics classroom. The third was ‘appropriate practical work’.
This referred to the need for learners to develop from having to handle objects (‘the concrete stage’) to a stage at which objects could be replaced by pictures or diagrams (‘iconic’) before progressing to entirely abstract reasoning (‘symbolic’).
Rite of passage
At present, the typical secondary classroom sees little in the way of practical maths. There are obvious organisational reasons for why this should be, but also often an unspoken assumption that ‘practical stuff’ ought to be left behind in primary school.
Yet we remember once observing a lesson in which top set Y8 pupils enjoyed cutting up cereal packets to measure their rectangular faces, before then computing their areas and thus the total areas of their packets. To our surprise, many pupils struggled with the same problem when it was posed in the form of an orthogonal projection with measurements given. Most pupils in the class were happy with manipulating abstract algebra, yet in this instance still needed recourse to concrete objects.
The rite of passage from ‘concrete’ through ‘iconic’ to ‘symbolic’ isn’t a simple progression in which learners just move on from one stage to another. All of us can benefit from moving backwards and forwards between those stages, but teachers of mathematics often won’t see any need to revert to the ‘concrete’ – and thus fail to notice that some of their pupils may benefit from doing so.
The logistical difficulties of organising practical work in secondary maths classrooms remain, but opportunities do exist. Such activities might include surveying certain areas of the school, such as the playing fields, or using card and scissor dissection of a circle to establish its area, as well as the usual trigonometry involved in finding the heights of buildings, trees, et al. We also shouldn’t forget other obvious examples, such as using string to estimate the circumference of a circle, dice-throwing and pencil/ruler/compass constructions.
Mathematical thinking
The benefits of practical work extend well beyond aiding cognitive development. It can motivate pupils, promote collaborative working, help develop manipulative skills and – since it involves the application of mathematics – support the development of essential modelling skills. By its nature, practical work encourages discussion and a more precise use of language, which is crucially important to developing mathematical thinking.
Those of a practical bent often tend to be good at improvising. It’s surprising, for instance, how useful it can be for a teacher to keep a knotted piece of string in their pocket (though make sure it has at least 12 sections before using it to explain Pythagoras). Who could teach vectors, or 3D Pythagoras, without using a corner of the room? Seeing their teacher ‘being practical’ will help pupils better appreciate how practical mathematics can be, and hopefully further develop their imaginations.
Practical work can then morph into technology-based assignments via the use of geometric tools and packages. If pupils are okay with the idea of ‘iconic’ learning, why issue pencils, rulers, compasses and protractors, when we can emulate their use on our whiteboards?
Pupils working at ‘even better if…’ can meanwhile try getting to grips with well-designed packages – for example, graph drawing packages, and the excellent interactive geometry packages available to support KS4 work on circle theorems.
Access to information
Among the aforementioned Cockcroft recommendations was the suggestion that every pupil should be able to access a calculator in mathematics lessons. Within a scant few years, that target had been met and surpassed to the extent that virtually every pupil had a calculator of their own.
Using a calculator is itself a practical skill, with programmable calculators offering some students greater possibilities and flexibility. Indeed, around the turn of the millennium it seemed as if the technology category as a whole was taking us to a place of ever increasing personal computing power – yet instead, smartphones arrived and shifted us away from the prioritising of computing power, in favour of prioritising access to information instead.
That does, however, at least mean that in the present day, the easy availability of spreadsheet packages such as Excel allows most pupils to access and use technology in their study of mathematics. Some of the most obvious uses are to be found in the study of statistics, and the logging, managing and display of data that this demands.
The computing power of Excel can, however, be brought to bear on probability as well, by having students use it to examine sample means. It takes only moments to enter 1,000 realisations of a uniformly distributed random variable into a spreadsheet column, and then copy these horizontally across 10 columns to produce 1,000 means of samples of size 10. From there, you can quickly generate a further 100 columns, giving 1,000 means of samples of size 100, and so forth.
A different assignment might call for the construction of a much more simple spreadsheet to compute a gradient and intercept of the line of best fit to just a few data points in the form (xi, yi), and compare them to values computed by Excel. The line can be displayed on a graph of the points, with the option to change the points at will.
This kind of construction is simple post-16 work, but can serve as a powerful introduction to probability modelling, while demonstrating the capabilities of spreadsheets. It also shows how statistics can be computed for reasons other than merely summarising data.
‘Wow’ factor
Then there are applications within mathematics. It’s very easy to use post-16 maths – the Taylor series, for example – as the basis for a very small spreadsheet that gives the sine of an inputted angle. Again, demonstrating this spreadsheet to KS4 pupils has a certain ‘wow’ factor, and will give them some insight into how their calculators do what they do.
Financial mathematics will often fail to inspire KS3/4 pupils, because the power of the relevant mathematics isn’t available to them yet. But Excel gives us a means of enacting repetitions, enabling us to explore the effects of compounding.
For instance, we could take an interest rate of 100% per annum and apply it to £1 (cut us some slack here). After one year, the result is £(1 + 1)1 = £2.
Now compound it twice a year. After one year, the result is £(1 + ½)2 = £2.25. Now generalise, put it into Excel, and see the result of decreasing the compounding interval. What’s interesting about it?
We’ll finish here with one of our favourite practical exercises – using Excel to explore the harmonic series:
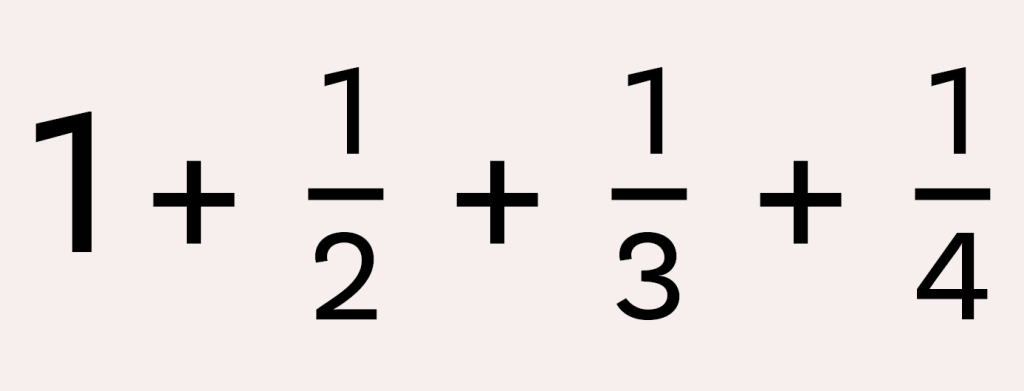
It diverges, but very slowly indeed! By setting the Excel calculations to run on a loop using Visual Basic for Applications, one can compute huge upper limits to the time needed to sum this to a given small total.
Once again, the act of demonstration can be used to ignite imaginations. That’s what we need to be doing when we teach mathematics – something that practical work and technology can
very much help us with
Seeing it in practice
We once observed a Y10 physics lesson in a girls’ school that involved pupils recording a measure of the classroom’s background radiation, and then compiling an Excel column of readings from other substances.
The awe and wonder of dealing with radiation soon paled into insignificance once the pupils were shown how the value of the background radiation could be subtracted from every other reading by just one pull-down menu.
Keith Parramore and Joan Stephens are a husband-and-wife team of mathematicians and visiting tutors to trainee teachers, both having previously taught mathematics in different school settings and held academic posts at the University of Brighton and University of Chichester respectively
Their book, Lessons Learned from Maths Lessons, is available now (John Catt Educational, £16)