KS2 maths – variation theory

John Bee explores how variation theory can help children understand similarities and differences in concepts and procedures…

- by John Bee
Variation theory draws attention to essential and non-essential properties of concepts. It focuses your attention on the variables in maths and considered similarities and differences.
Used accurately, it can be a transformative pedagogical approach to unlock the maths curriculum for all learners.
First, we need to be careful that we do not confuse variation with variety. Most lessons offer a variety of different activities for children to engage with. Variation needs careful and deliberate choices on what to vary and when to vary it.
Conceptual and procedural variation
There are two different types of variation theory: procedural and conceptual.
Conceptual variation draws attention to the essential features, to the essence of the concept by varying the non-essential features. The example below shows an octopus and a non-octopus (a cuttlefish).

Here, we are forced to think about what makes an octopus an octopus and not a cuttlefish. Even though there are certain similarities, there are many differences.
- Similarities: live in water, change colour, move by jet propulsion, have eight arms.
- Differences: Cuttlefish have backbones, octopuses have a round head but cuttlefish are triangular.
In a maths context, this can support children’s understanding of key concepts. For example, when learning about the concept of a triangle, using examples and non-examples can draw attention to the essential and non-essential features of a concept:

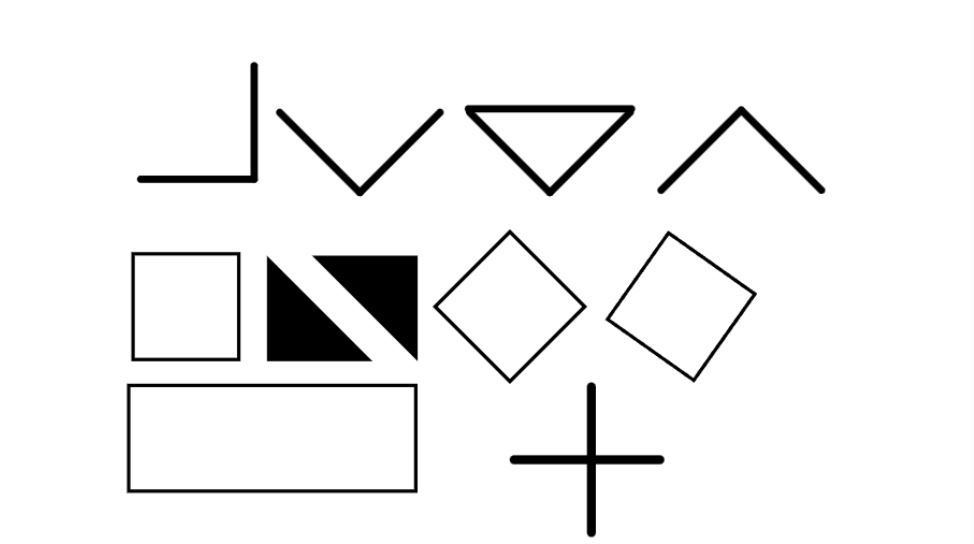
Similarly, in KS2, when learning about right angles, children may only ever see right angles presented in standard ways. Try showing pupils alternative models, such as these:
Finally, imagine you are beginning to teach fractions for the first time and you are introducing the concept of ¼.
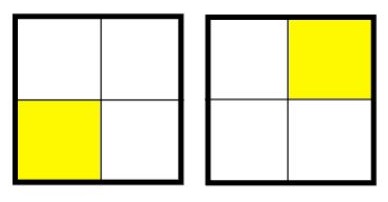
Showing a representation like the one here may lead children to think that ¼ is a square, it is yellow, it is a part, it is in the top right of a shape.
Now imagine, a quarter was presented as follows and preceded by asking: ‘What’s the same, what’s different?’
Here, children can generalise that there are 4 parts and so one part is a quarter.
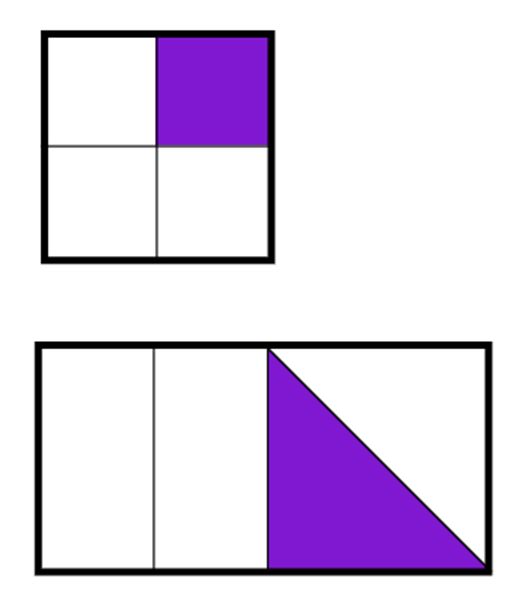
Now imagine, we add in a non-example to compare the concept of ¼.
Using these images, children can deepen their understanding by considered fractions as being equal parts of a whole.
Procedural variation draws attention to patterns and generalisations, quite often in number. It links one calculation to the next and establishes a connections and pattern.
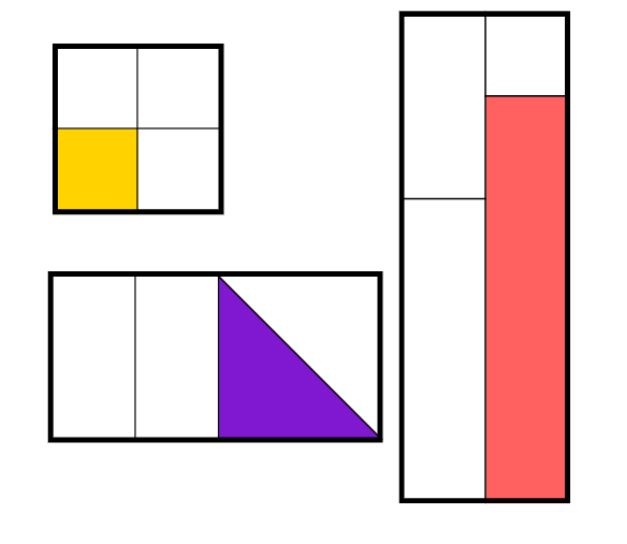
Asking, ‘what is the same, what is different?’ can be a powerful approach in the classroom as it focuses attention on patterns, links and connections.
Taking this further, you could present children with calculations such as:
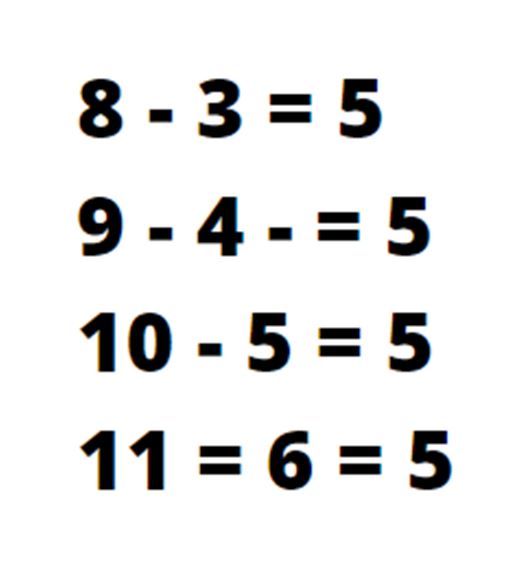
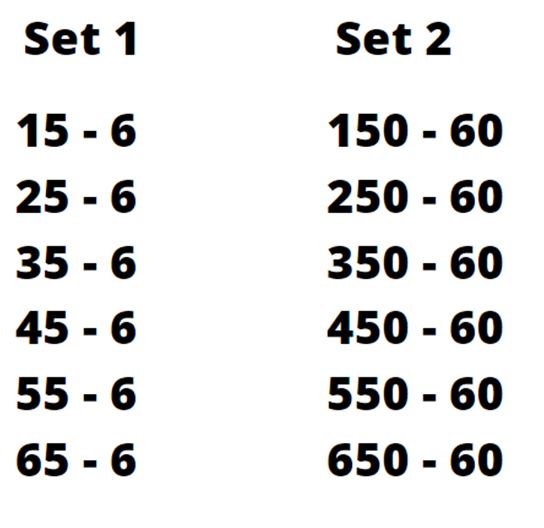
Children may draw attention to the difference being five each time. Asking children to continue this or find as many numbers as possible with a difference of five can be a powerful learning experience.
Children may be able to generalize that 12 – 7 = 5 as it follows the pattern or that 7 – 2 = 5 as this precedes the pattern.
Deepening their thinking could lead to decimals such as 8.1 – 3.1 = 5 and so 8.2 – 3.2 = 5 and therefore 8.11 – 3.11 = 5 too.
Here, the careful and deliberate variation of the numbers leads children to expose the underlying structure of difference.
If, then, so
Introducing procedural variation for the first time in the classroom takes time. Children need to learn to look at maths in a completely new way and need to be explicitly taught to expose mathematical patterns and structures.
In the example below, the factors have been varied to impact on the product.
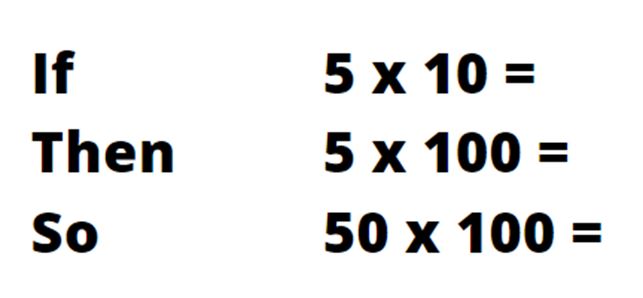
You could ask children how they might work out 500 x 100 or 0.5 x 100 or take a more general approach and ask children what is the same, and what is different and then ask what other calculations pupils can derive from the sequence.
Once children have practiced this, they may begin to design some questions of their own.
Variation theory focuses thinking on essential and non-essential properties. It allows children to think deeply about mathematical concepts and make connections, patterns and links.
John Bee is head of KS2 and maths leader at a primary school. Follow John on Twitter @mrbeeteach and see more of his work at mrbeeteach.com