How important is maths practice?

Repetitive learning of sums and examples of perfect shapes are only half the equation, says Jo Boaler

- by Jo Boaler
“Don’t students need a lot of maths practice?”
Parents often ask this question when I show them the evidence that pupils need to engage in mathematics both conceptually and visually – by which they mean “Shouldn’t they be doing pages of maths questions in isolation?” And it raises an interesting point – how much practice (if any) do students need in mathematics?
A great disservice
We know that when learning happens a synapse fires, and that we need to revisit ideas and learn them deeply in order for structural brain change to happen. But what does that mean, exactly?
Yes, it’s important to revisit mathematical ideas, but the ‘practice’ of methods over and over again is actually unhelpful. The most effective means of reinforcing a new idea in maths is actually to use it in different ways.
When we pull out the most simple version of an idea and give students 40 questions that repeat it, we’re doing them a great disservice. It turns students away from maths, it’s unnecessary and it does not prepare them to use the idea in different situations.
In Malcolm Gladwell’s bestselling book Outliers, he develops the idea that it takes roughly 10,000 hours of practice to achieve mastery in any given field. He describes the achievements of famous musicians, chess players and sports stars, and he highlights something hugely important – while many people think of figures such as Beethoven as natural geniuses, Gladwell shows these people have to work long and hard to achieve their great accomplishments, with a growth mindset that supports their work.
Unfortunately, I’ve spoken to a number of people who have interpreted Gladwell’s idea to mean that students can develop expertise in maths after 10,000 hours of mindless, repetitive practice. This is incorrect. We do not need students to take a single method and practice it over and over again. That is not mathematics; it does not give students the knowledge of ideas, concepts, and relationships that make up expert performance.
Someone working for 10,000 hours would need to be working on mathematics as a whole – considering mathematical ideas and connections, solving problems, reasoning and connecting methods.
The most simplified version
In the United States, most textbook authors base their whole approach on the idea of isolating methods, reducing them to their simplest form and practising them. This is problematic for many reasons. First, it induces boredom in students; many will simply switch off when they think their role is to passively accept a method (Boaler and Greeno, 2000) and repeat it over and over.
Second, most activity examples give the most simplified and disconnected version of the method to be practised, giving students no sense of when or how they might use it.
This problem extends to the ways in which books introduce examples of ideas, always giving the most simple version. The following shows the answers students give to maths problems in research studies, highlighting the nature of the problem caused by textbook questions.
Eleven-year-olds were shown the following figure and asked: is line A parallel to line C?
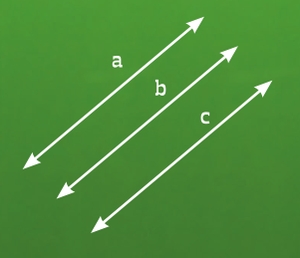
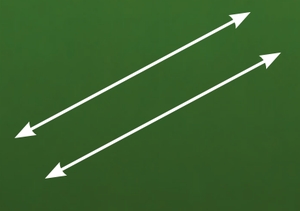
Most answered, “No, because line B is in the way.” This comes about because the concept of parallel lines is almost always illustrated by a picture of two lines like this:
Students were then asked to name the following shape:

Most were unable to. The shape is a hexagon (a six-sided polygon), but hexagons are almost always shown in this way:

This does not illuminate the full concept of a hexagon well.
Trending
Over half of eight-year-olds did not see the following as examples of a right angle, a triangle, a square or parallel lines:
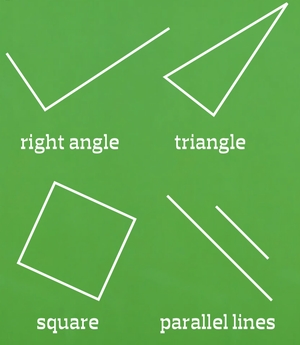
This is because they have always been shown the simplest version of the concepts. This is the familiar view that students expect to see:
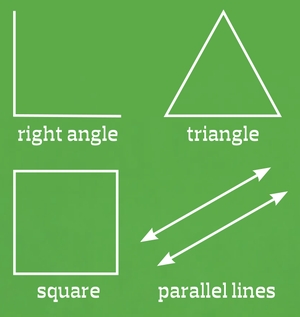
The fact that over half of the students in the studies could not name the shapes tells us something important – when textbooks introduce only the simplest version of an idea, students are denied the opportunity to learn what the idea really is.
Students were unable to name the different examples because the textbook authors had given ‘perfect’ examples each time. When learning a definition, it is helpful to offer different examples – some of which barely meet the definition, and some of which do not meet it at all.
‘Non-examples’
Mathematics teachers should also think about the width and breadth of the definitions they’re offering, and whether these might be better highlighted by ‘non-examples’, i.e. when learning a definition, it is often very helpful to see both examples that fit the definition and others that do not, rather than just presenting a series of perfect models.
For example, when learning about birds it can be helpful to think about bats and why they are not birds, rather than to see hundreds of examples of sparrows and crows.
The misconceptions that students form when shown perfect examples is analogous to the problems they develop when practising isolated methods over and over. Learners are given uncomplicated situations that require the simple use of a procedure (or often, no situation at all). They learn the method, but when they are given realistic mathematics problems, or when they need to use maths in the world, they are unable to use these methods.
Real problems often require the choice and adaptation of methods that students have never even thought about, let alone learned to use.
Additional mindsets
Help children see maths as thinking, sense making, big ideas and connections – not the memorisation of methods…
One excellent method for preparing students to think and learn in these ways is a strategy called ‘number talks’. It was developed by Ruth Parker and Kathy Richardson, and is an ideal short teaching activity you can use to start lessons with, or that parents can use at home.
It involves posing an abstract maths problem and asking students how they solve the problem mentally. The teacher then collects the different methods students give and looks at why they work. For example, a teacher may pose 15 x 12 and find the students solve the problem in these five different ways:

This is an edited extract from Mathematical Mindsets: Unleashing Students’ Potential through Creative Math, Inspiring Messages and Innovative Teaching by Jo Boaler (2016, £13.99, Jossey-Bass)
Jo Boaler is a professor of mathematics education at Stanford University; for more information, visit www.youcubed.org or follow @joboaler