Head First – Are We Making KS2 Maths Harder Than It Needs To Be?

Did the final question on the 2016 SATs test have your pupils stumped? Then it᾿s time we helped them reason their way to simpler solutions, says Mike Askew…

- by Mike Askew
Developing reasoning skills is one of the core aims of the new curriculum – so why does children᾿s ability in this regard lag behind their ability to calculate?
We now have access to the question level results of the 2016 National Tests for KS2 mathematics, and as you might expect, there are some interesting outcomes. Take, for example, the question that presented children with the statement 5542 ÷ 17 = 326. Pupils were asked to explain how they could use this result to find the answer to 326 x 18.
Only 33% of pupils were able to answer this correctly, and that figure is based on the number of learners attempting the question. Taking into account the 21% who left it unanswered, the success rate for all learners taking the test drops to 26%. Admittedly, this was the last question on the third paper (the second of the two ‘Reasoning’ papers) and so presumably was expected to be a difficult.
‘Gifted’ with the ability
Another question that involved reasoning about division and multiplication asked children to figure out the missing number in the following equation: 70 ÷ [ ] = 3.5
The statistics here show a similar pattern – an overall success rate of 32%, with 87% of learners attempting the question and 37% of this number getting it correct.
The figures regarding ‘bald᾿ calculation problems, however, tell a different story. Take the following example from the test paper: 1320 ÷ 12. A full 95% of all pupils attempted the question, with 86% getting it right (an overall success rate of 82%). And what about this long division problem:
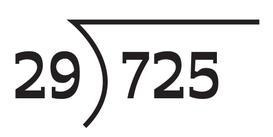
Although a late question on the arithmetic paper, 93% of children attempted it, with 67% getting it correct (an overall success rate of 62%).
So should we be celebrating pupils’ success in carrying out calculations they will probably never have to do in real-life (who doesn᾿t have a mobile phone with a calculator to hand)? Or should we be worried about the poor results that reveal pupils’ difficulties in reasoning about the relationship between multiplication and division? And why are there such disparities?
We can speculate about the different causes that lead to such results. As noted above, ‘326 x 18’ was the last problem of all three papers, so maybe the low score is a reflection of the commonly held belief that only a few pupils have been ‘gifted᾿ with the ability to reason mathematically.
On the other hand, if we buy into the idea that the majority of pupils are capable of ‘mastering’ mathematics, then we have to assume – until proven wrong – that everyone can become as successful at reasoning mathematically as calculating. And we have to look at how we can help everyone to achieve this – at whether our teaching achieves the right balance between the two skills.
Can I do this mentally?
In a small-scale piece of research carried out just after pupils took the National Tests this year, Hamsa Venkat – my colleague at Wits University – interviewed a group of English Year 6 pupils, during which she asked them if they could answer 375 + 99 and 435 – 399.
Most of them worked on each problem using a vertical algorithm. Reaching for a pencil to calculate 375 + 99, one girl explained that “I find it easier to work it out on paper ‘cos I can see what I am doing. It won᾿t get clogged up in my head.’ Later, the same pupil pointed out that 435 – 399 had to be done on paper, because “the units in 435 were smaller than the ones in 399”.
If you are trying to carry out a written vertical algorithm in your head, then 375 + 99 is certainly going to clog up your working memory. But adding on 100 to 375 and then taking off one is surely simpler? 399 is so close to 400 that subtracting 399 from 435 is not a big deal, mentally speaking – isn’t that something we would like learners to spot?
The 1999 National Numeracy Strategy [PDF] provided some sound advice in this regard, arguing that before working on any calculation, pupils should first ask themselves – ‘Can I do this mentally?’
Rigid thinking
One of the ‘selling points’ for the resurgence of written algorithms, including long division, is that learning these methods also helps develop conceptual understanding – but the results on the multiplication and division question I discuss above belie this claim.
Being good at long division does not, yet at least, appear to help learners develop conceptual understanding of the relationship between multiplication and division. Although we don’t yet have examples of what pupils actually did in the tests, I suspect that knowledge of long division may actually have got in the way of pupils working flexibly with 5542 ÷ 17 = 326.
Of the fifth of learners who did not attempt this question, I wonder how many of them looked at it and thought, ‘Hmm, long division…I can’t do that’. Of the 55% or so who attempted the question but got it wrong, how many tried to actually carry out a calculation?
Don᾿t leave it too late
Unpacking the reasoning behind this question reveals an important insight: the thinking involved in getting an answer can be started much earlier than in Year 6.
Take 24 ÷ 4 = 6. We expect that pupils in lower Key Stage 2 can use an equation like this to derive related facts, such as 6 x 4 = 24. We can therefore work with younger children to play with this.:
If 6 x 4 = 24 then 6 x 5 = 6 x 4 + 6
Or, if 360 ÷ 9 = 40, then, 40 x 9 = 360
And so 41 x 9 = 40 x 9 + 9 = 360 + 9
Or if 5542 ÷ 17 = 326, then 326 x 17 = 5,542, and so 326 x 18 = 326 x 17 + 326
If pupils have been reasoning around ‘If I know this, then what else can I derive?’ approach throughout their learning of mathematics, then perhaps 5542 ÷ 17 = 326 could be one of the easiest questions on the test. After all, the ability to reason is independent of the size of the numbers involved.
To take another example, adding or subtracting by rounding to a multiple of 10 means I may be able to add 4.345 + 9,999 long before I can add 85 + 76!
Similarly, a key part of successfully answering 70 ÷ [ ] = 3.5 has to be the recognition that 70 and 3.5 are not randomly chosen numbers: if the echoes of 3.5 being half of 7 come to mind, then it is a short step to reasoning that if 7 ÷ 2 = 3.5 then 70 ÷ 20 = 3.5.
We know from research that another consequence of over-emphasising standard methods is that learners do not pay attention to the numbers in the calculation. But in all these reasoning questions, it is understanding the relationship between the numbers – not the numbers themselves – that makes for success.
When looking at the KS2 test, it is important for school to look through the size of the numbers involved (‘Year 3 don’t do 5,542 ÷ 17 = 326; we᾿ll leave that for Year 5 or 6′) and ask what needs to be done across all the years to help learners develop their reasoning skills.
Teaching: imparting or interacting?
Part of the attraction of teaching calculating procedures is that they are, well, teachable – in the sense that we can demonstrate a method and then get pupils to practice it until it has been committed to memory.
But while I can show someone how to carry out a calculation, I cannot, in the same way, show them how to reason about a mathematical relationship. Teaching for reasoning has to be different.
As a teacher, I can provide opportunities to reason and then engage the learners in dialogue about that reasoning. In doing so, I have to consider a longer time span than the single lesson. The first time that a class encounters something like ‘If 360 ÷ 9 = 40, what else can we figure out?’ the responses may be quite limited. But if such challenges are a regular part of the classroom conversation, then the range of possibilities grows.
If you accept, as I do, that much of mathematics is about developing ‘habits of mind’, then we have to look at what sort of habits those might be. The girl I discussed earlier seems to be developing the ‘habit of mind’ that any calculation with large numbers has to be done with paper and pencil. Perhaps more productive ‘habits of mind’ include things such as asking yourself ‘Is there a simpler calculation I could do?’ and ‘If I know this mathematical fact, then what else can I figure out?’
In other words, pause and think before reaching for the paper and pencil.
Hard times
Are written procedures making maths unnecessarily difficult?
Writing back in 1994, Eddie Gray and David Talli from Warwick University noted some differences between pupils who relied on using a set procedure for calculating and pupils who could use flexible approaches.
Not only was the attainment of the pupils focused on procedures lower than that of the flexible thinkers, but the authors argued that the procedural thinkers were actually engaged in a more difficult form of mathematics, which contributed to the difference in attainment.
If the introduction of the arithmetic paper in the National Tests is leading to a renewed emphasis on written procedures over mental strategies, then we have to ask ourselves an important question. Could an unintended consequence of this approach be that we are making mathematics more difficult than it needs to be?
Mike Askew is adjunct professor of education at Monash University, Melbourne and a freelance primary maths consultant; for more information, visit www.mikeaskew.net or follow @mikeaskew26