Encourage Independent Thinking in Primary Maths

We need to think carefully about the activity that a task will generate, says Mike Askew

- by Mike Askew
- Educator, researcher and speaker with a focus on primary maths education Visit website
Visiting a classroom years ago, my attention was caught by a Y4 girl called Meg.
She was doing a page of subtractions, all laid out in the standard vertical form:
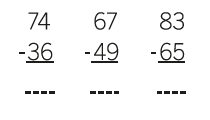
Watching her work, I was struck by the fact that she was writing in correct answers without showing any working, but her moving lips suggested she was talking through her method to herself. I asked her to explain how she was finding answers. For the first example, her explanation went along the lines of:
“I can add 4 to 36 to make 40, and from 40 to 74 is another 34. So 4 plus 34 is 38. The answer is 38.”
In other words she was finding the difference between the two numbers by counting up from the smaller number to the larger, confidently doing it in her head (with the help of some self-talk).
The reason I remember her so well is that when I came back to her desk a little later, she had changed all of her records so that they looked like this:
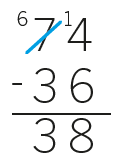
When I asked her why she’d done it, she said, “Because my teacher likes it to look like that!”
Rich maths task ideas
When talking about what pupils are asked to do in mathematics lessons, the terms ‘tasks’ and ‘activity’ are used fairly interchangeable. I find it helpful, however, to keep them separate, in the sense put forward by the writers Christiansen and Walther in the 1980s.
They argued that ‘task’ is what pupils are asked to do, ‘activity’ being what they subsequently actually do, mathematically in particular. For me, keeping ‘task’ separate from ‘activity’ helps in several ways.
Meg’s story demonstrates the first benefit of keeping task and activity separate – it helps me remember that even if a pupil produces correct answers with apparently correct working, that is no guarantee of what they actually did.
Presumably, the teachers’ expectation in Meg’s lesson was that the task of answering the subtractions would be done through the activity of the decomposition method. Meg’s final page of working would have given the impression that that was precisely what she had done.
But while written results give some impression into pupils’ mathematical activity, it is really only through talking with them that we get real insight into their thinking.
The second thing that separating ‘tasks’ and ‘activity’ helps with is in examining tasks and asking myself whether or not the subsequent mathematical activity asked for is the most sensible. Take this example that is similar to a problem I came across recently:
Mrs Jones bought these boxes of pencils
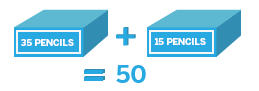
Miss Smith bought these boxes of pencils

Use the answer to the total number of pencils that Mrs Jones bought to work out how many more pencils Miss Smith bought.
I think the task writer expected pupils to do something like:
35 + 15 = 50
15 + 55 = 15 + 35 + 20 = 50 + 20, so Miss Smith bought 20 more pencils.
Given the problem setup, surely the ‘smart’ activity is to notice that both teachers bought a box of 15 pencils, so only the boxes of 35 and 55 need be compared, and that the latter has 20 more pencils.
To solve the task of how many more pencils Miss Smith bought, I do not really need to engage in the activity of working out overall totals.
A primary aim of mathematics teaching is, for me, to encourage pupils to think independently – considering the activity they are likely to engage in for any given task helps me judge whether a task will encourage independence of thought or whether it only expects pupils to do what someone else thinks.
Following on from this, a third payoff is in thinking about whether a task has the potential to engage pupils in the activities of mathematical problem solving and reasoning, or whether it is simply expecting them to reproduce a pre-determined method.
In other words, I want there to be something of a ‘gap’ between a task and the pupils’ activity, and, if these are likely to be too close together, to think about how the task can be tweaked to open up the activity (you can read more about this in my book Transforming Primary Mathematics).
Trending
One productive way of developing tasks to encourage rich mathematical activity is to get the pupils to generate examples. Take something like a page of subtraction examples, such as Meg was working on. A simple way to increase the range of mathematical activity is to put up numbers from which pupils create their own examples.
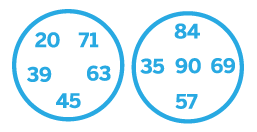
Choose a number from each circle to make up and answer a subtraction calculation. Make up and answer nine more subtractions in this way.
The pupils’ activity now involves not only calculating subtractions, but also setting them up, and the numbers that pupils choose to use would give me, the teacher, a sense of what subtractions they are confident in doing. I could push the task further in this direction:
Choose a number from each circle to make up a subtraction calculation. Make up five subtractions that you think are easy and you can answer mentally. Make up five subtractions that you think you need to work out using paper and pencil. Answer your calculations.
Of course there is now a cost-benefit to the teacher – the time I’ve gained in planning by not having to create a worksheet is going to be eaten up in marking 30 different sets of calculations. On the premise that I want the pupils to be doing most of the thinking in a lesson, I can turn this to my, and their, advantage. As above, they make up ten calculations, but instead of answering them the task would be:
Swap your 10 calculations with your partner. Answer your partner’s calculations. Swap back and mark the calculations you set.
Now pupils now get to answer twice as many calculations (thanks to the marking) and everything is also set up for a productive class dialogue on what made some subtractions easy, and what made some harder. Following are some more examples of how a task can be played with to open up more opportunities for mathematical activity.
Open-ended maths activities
This is a popular activity based on the number game made famous on the TV show. A simple set up for this is to take a die and roll it four times to create four digits to work with. Then roll it again to make a three digit target number. For example:
Using 2, 2, 5, 6 in any combination, can you make 154?
As it stands, this is a nice task but you either succeed or you don’t. And if you get the answer quickly, what then? A simple tweak is to open up the target. There are many ways that this could be done:
- How many multiples of 10 can you make?
- Make three different calculations and put the answers in order.
- Can you make two calculations with answers that are consecutive?
- Three consecutive answers?
- What’s the longest string of consecutive numbers you can make?
- Can you find answers that are multiples of 3 and 5?
- How many numbers between 100 and 200 can you make?
You get the idea. The possibilities are limitless and the range of mathematical activity is greater.
Symmetrical shapes
A typical task would be to identify which shapes have line symmetry given a collection such as:

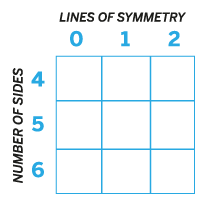
A task that would get pupils engaged in activity of thinking deeply about symmetry would be to see if they can create nine polygons to fill the grid below. If they think any cell cannot be filled, can they explain why?
Fractions
A typical comparing fraction task would be something like:
In each pair, circle the larger fraction:
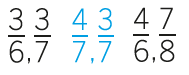
The task could be changed to engage learners in more mathematical activity:
For each of the challenges below, choose four digits from the following list to make a pair of fractions (you cannot use the same digit twice in any one challenge): 2, 3, 4, 6, 7, 8
- A pair of fractions that are equal.
- A pair of fractions where one is larger than the other. Make up three pairs like this.
- Use all six digits to make three fractions. Put them in order from smallest to largest. Do this three different ways.
Division
Rather than provide examples, get pupils to make some up, given some constraints:
Make up three different division calculations that each have the numbers 2 and 12 in them. Write a word problem to go with each of your calculations.
This would also work with any of the four operations. At the core of teaching mathematics is the question of how best to help pupils make mathematical sense of their experiences. Providing tasks for them to do is part of this: considering the activity then engaged in helps us decide whether or not the tasks are doing their job.
Mike Askew is adjunct professor of education at Monash University, Melbourne. A former primary teacher, he now researches, speaks and writes on teaching and learning mathematics. Find him at mikeaskew.net and follow him on Twitter at @mikeaskew26.