Maths puzzles – 42 summer holiday teasers for KS3/4

42! It's the answer to 'how many days are there in six weeks?' as well as 'Life, the Universe and everything'…

- by Teachwire
- Classroom expertise and free resources for teachers

We’ve picked out 42 maths puzzles, one for each day of the six-week holiday (even though it’s very unlikely students will have exactly six weeks off).
Give students this link before they leave for the year, or email each question out a day at a time if you have the patience.
Day 1 | 12 to 15
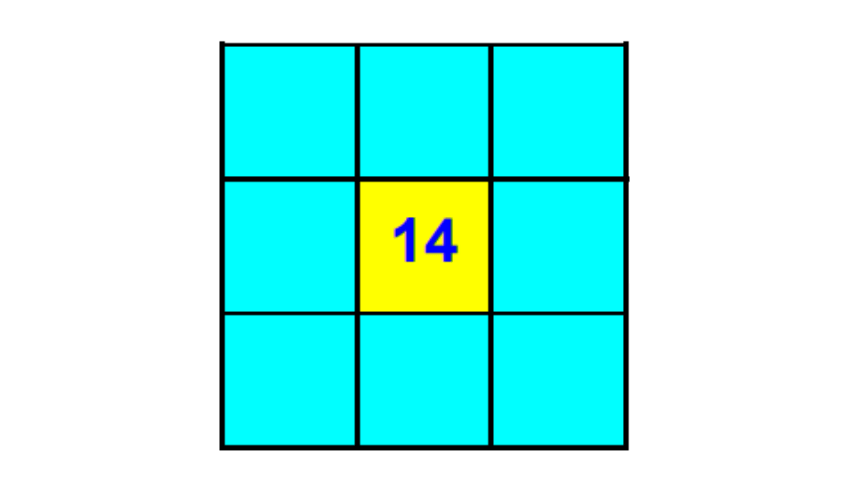
Can you put the numbers 1 to 8 in each of the squares so that each side adds up to middle number?
Try more of these puzzles at MathSphere and take a look at the answers too.
Day 2 | Puzzling Taxi Fares
Two salespeople (A and B) hired a car to take them from their office to their customers.
A’s customer lived 10km away from the office.
B’s customer lived 20km away from the office.
The road to B’s customer went directly past A’s customer.
The trip cost £20 in total.
What part of the bill was it fair for each salesperson to pay?
Get worksheet and Powerpoint versions of this puzzle and check out the answers.
Day 3 | 24 from 8, 8, 3, 3
How can you get the answer 24 by only using these numbers:
8, 8, 3, 3
You can use add, subtract, multiply, divide and parentheses.
Bonus rules: you can also use logarithms, factorials and roots
Day 4 | Weighty problem maths puzzles
I have ten boxes with a total weight of 75kg
- 15kg
- 13kg
- 11kg
- 10kg
- 9kg
- 8kg
- 4kg
- 2kg
- 2kg
- 1kg
I want to pack the boxes into three crates. Each create can carry a maximum of 25kg.
How can I pack the boxes into the crates?
(There may be more than one way).
Check out this puzzle on Math is Fun and look at the answer too.
Day 5 | Absolutely Christmas crackers
A make-your-own Christmas cracker kit contains:
- Three colours of hat: red, yellow, blue
- Four prizes: toy car, spinning top, magnifying glass, mini hairbrush
- Four different jokes
All the other parts are the same.
The kit contains enough bits for 50 crackers. Can you make all the crackers different to one another?
This is another one from Math is Fun. View the answers here.
Day 6 | Roll the dice
Read people’s answers to this one under the original tweet from Ben Orlin.
Day 7 | Game on
Sergio is playing two different games on the computer: game 1 and game 2.
The two events are independent.
The tree diagram shows some of the information below.
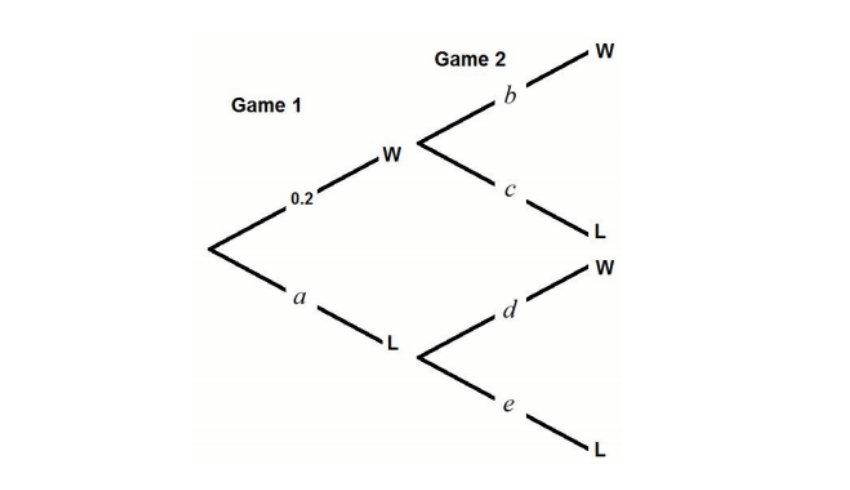
Given that the probability of Sergio losing both games is 12/25, find the values of a, b, c, d and e.
View this problem and more GCSE ‘wordy’ problems at m4ths.com, as well as the answer.
Day 8 | Compound rectangular shapes
Sami worked out the area of the orange shape as 10 x 4 + 8 x 7 = 96cm2.
Razina worked out the area as 12 x 7 + 3 x 4 = 96cm2.
Lukas worked out the area as 10 x 10 – 2 x 2 = 96cm2.
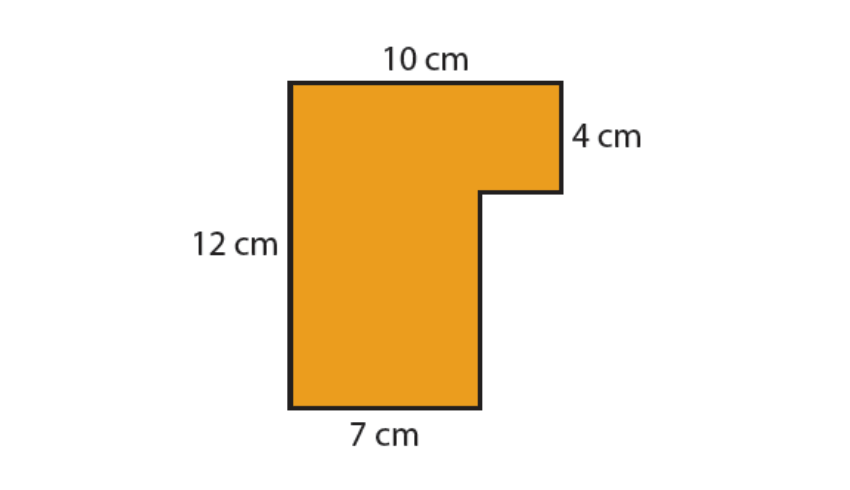
Are you convinced by Sami, Razina or Lukas’ reasoning? Explain your answer.
View this puzzle on Don Steward’s blog.
Day 9 | The stupid gardener
A gardener planted a row of 100 strawberry plants in his garden, setting them exactly 1m apart.
Each plant produced just one strawberry.
When picking time came, the stupid gardened placed a basked 1m from the end of the row. He then proceeded to pick and carry each strawberry to the basket, one by one.
Starting and ending at the basket, how far had the gardener walked when he finished picking all 100 strawberries?
Download this puzzle as Worksheet and PowerPoint versions, and view the answer.
Day 10 | 1996 puzzle
Use the numbers 1, 9, 9 and 6, exactly in that order, to make the following numbers:
- 28
- 32
- 35
- 38
- 72
- 73
- 76
- 77
- 100
- 1000
You can use the mathematical symbols +, −, ×, /, √, ^ (exponent symbol) and brackets.
Example: 1 × 9 + 9 × 6 = 63
View this puzzle on Math is Fun, where you’ll also find the answer.
Day 11 | Dizzy digits maths puzzles
This puzzle is in three parts. You need to answer all three parts.
Part 1: Use four 4s to make 44
Part 2: Use five 5s to make 55
Part 3: Use six 6s to make 66
You can use any of the +, −, x , ÷ and = keys.
These maths puzzles are from MathSphere. View it and the answer here.
Day 12 | Medal muddle
Thirteen nations competed in a sports tournament. Unfortunately, we do not have the final medal table, but we have the following pieces of information:
1. Turkey and Mexico both finished above Italy and New Zealand.
2. Portugal finished above Venezuela, Mexico, Spain and Romania.
3. Romania finished below Algeria, Greece, Spain and Serbia.
4. Serbia finished above Turkey and Portugal, both of whom finished below Algeria and Russia.
5. Russia finished above France and Algeria.
6. Algeria finished below France but above Serbia and Spain.
7. Italy finished below Greece and Venezuela, but above New Zealand.
8. Venezuela finished above New Zealand but below Greece.
9. Greece finished below Turkey, who came below France.
10. Portugal finished below Greece and France.
11. France finished above Serbia, who came above Mexico.
12. Venezuela finished below Mexico, and New Zealand came above Spain.
Can you recreate the medal table from this information?
Can you describe an efficient strategy for solving problems like this?
This puzzle is from the NRICH website. Look here for approaches, key questions, extensions and support.
Day 13 | Tea cups maths puzzles
Aunt Jane has bought a whole lot of cups and saucers. There are four sets:
- white
- red
- blue
- green
In each set there are four cups and four saucers (16 cups and 16 saucers altogether).
You decide to mix them around so that there are 16 different-looking cup/saucer combinations laid out on the table in a very long line.
So, for example:
a) there is a red cup on a green saucer but not another the same, although there is a green cup on a red saucer
b) there is a red cup on a red saucer but that’s the only one like it
There are these 16 different cup/saucer combinations on the table. and you think about arranging them in a big square. Because there are sixteen, you realise that there are going to be four rows with four in each row (or if you like, four rows and four columns).
Here is the challenge: place these 16 different combinations of cup/saucer in a four by four arrangement with the following rules:
- In any row there must only be one cup of each colour
- In any row there must only be one saucer of each colour
- In any column there must only be one cup of each colour
- In any column there must be only one saucer of each colour
View the full puzzle on the NRICH website.
Day 14 | Insert 1-15
Day 15 | Place the 12 numbers
Day 16 | Bavarian
One glass has 10cl of tonic water and another 10cl of fernet.
Pour 3cl of tonic into the glass with fernet. After mixing thoroughly, pour 3cl of the mixture back into the glass with tonic water.
Is there more tonic in the glass of fernet or more fernet in the glass of tonic? (Ignore the chemical composition!)
View this puzzle and more on BrainDen, as well as the answer.
Day 17 | The puzzled farmer maths puzzles
A farmer set out to market with a turkey, a fox and a basket of wheat.
When he came to the river, he found there only an empty rowing boat, so small that he could only carry one thing with him at a time.
If the fox was left with the turkey, he would eat it. If the turkey was left with the wheat, she would eat it.
How did the farmer get them all across safely? What is the minimum number of crossings necessary?
Download worksheet and Powerpoint versions of this classic puzzle, and look at the answer.
Day 18 | Algebra cow
Solve the following (each letter is a digit):
COW x COW = DEDCOW
Day 19 | Five card trick
I am thinking of one of these five cards:
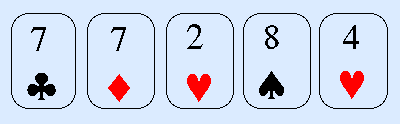
You have to try to find out which one I am thinking of. Here are some clues:
- The value of my card is a prime number
- The values of my two neighbours add up to a multiple of 3
- My card is next to a card which is next to the 2 of hearts
See this problem and the solution at Math is Fun.
Day 20 | Tricky twenty triangle
Put the numbers 1-9 in the boxes below so that each side of the triangle adds up to 20.
Trending
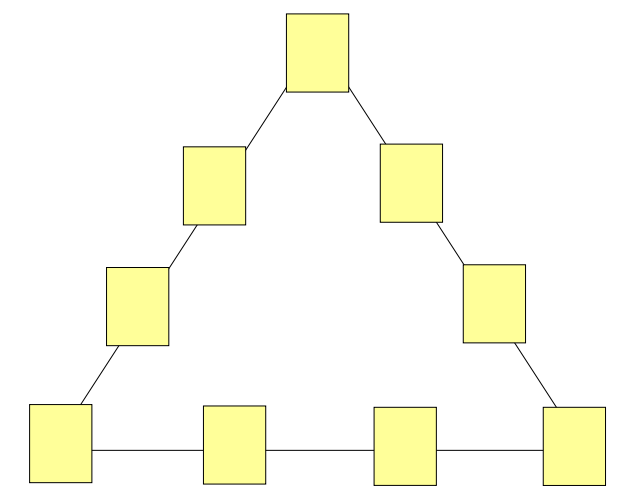
View this puzzle and the solution at Maths Sphere.
Day 21 | Working with ratios
In a factory the ratio of men to woman is 2:3.
The ratio of right handed men to left handed men is 7:3.
The ratio of right handed women to left handed women is 11:1.
What proportion of the people working in the factory are right handed?
View this problem and the answer.
Day 22 | Give me a hand
A professor and their spouse are at a party. At the party there are four more couples (five couples overall).
During the party, couples shake hands with the following rules:
- One does not shake hands with oneself
- One does not shake his/her spouse’s hand
At the end of the party the professor asked all the other guests at the part (including their spouse) how many different people they shook hands with. Each person tells him a different answer (meaning, if one person said “five”, no one else said “five”).
With how many people did the professor shake hands?
Day 23 | Bridge over troubled students
There are four men who want to cross a bridge. They all begin on the same side. You have 17 minutes to get all of them across to the other side.
It is night. There is one flashlight. A maximum of two people can cross at one time. Any party who crosses, either one or two people, must have the flashlight with them.
The flashlight must be walked back and forth, it cannot be thrown, etc. Each man walks at a different speed. A pair must walk together at the rate of the slower man.
Man 1: 1 minute to cross
Man 2: 2 minutes to cross
Man 3: 5 minutes to cross
Man 4: 10 minutes to cross
For example, if Man 1 and Man 4 walk across first, 10 minutes have elapsed when they get to the other side of the bridge.
If Man 4 returns with the flashlight, a total of 20 minutes have passed, and you have failed the mission.
This puzzle is from Steve Miller’s Math Riddles.
Day 24 | Three spinners maths puzzles
The 3 spinners below are each spun once and the number written down.
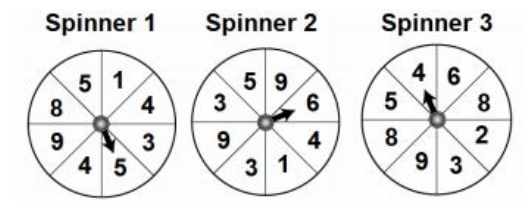
Find the probability that when the three spinners are spun, the numbers are either all prime numbers or all cube numbers.
View this problem and the answer at M4ths.com.
Day 25 | Pipes and pathways
These three houses are putting in gas, to be piped from the containers shown.
House A must be connected with container F, house B with D, and house C with E.
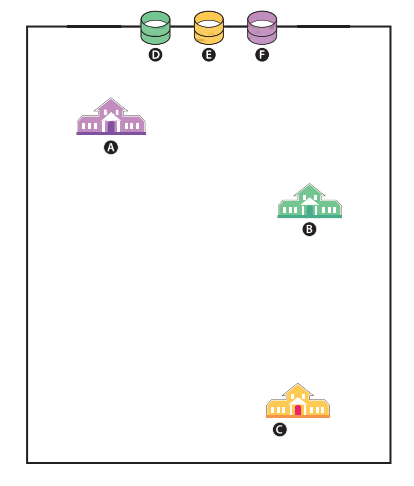
A clause in the title deed forbids laying one pipe across another, and owners of land around this plot refuse to allow the pipes onto their land. How will the gas company lay the pipes?
View this puzzle and the solution.
Day 26 | Monk steps
A monk has a very specific ritual for climbing up the steps to the temple.
First he climbs up to the middle step and meditates for 1 minute.
Then he climbs up 8 steps and faces east until he hears a bird singing.
Then he walks down 12 steps and picks up a pebble.
He takes one step up and tosses the pebble over his left shoulder.
Now, he walks up the remaining steps three at a time which only takes him 9 paces. How many steps are there?
View the solution at Braingle.
Day 27 | Circles maths puzzles
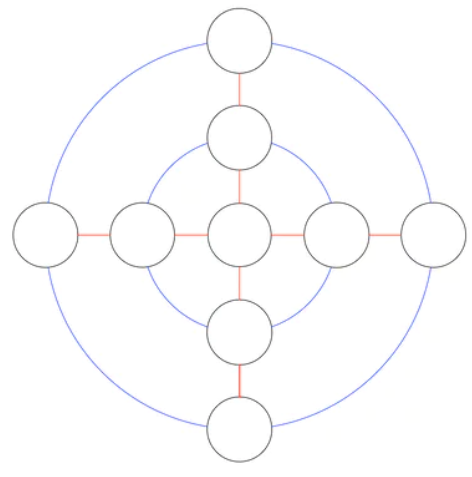
Write the numbers 1-9 in the black circles so that the sum of the numbers around each blue circle (and including the centre circle) and along both horizontal and vertical lines is the same.
View the solution at the Guardian.
Day 28 | Head over tails
Put four coins on table, in a row, all tails up.
Turn any three coins over: this counts as one move. You must turn three different coins to complete one move.
How many moves will it take to get all the coins on heads?
View the answer at Math Sphere.
Day 29 | Two jugs maths puzzles
You have an 8 litre jug full of water and two smaller jugs, one that contains 5 litres and the other 3 litres.
None of the jugs have markings on them, nor do you have any additional measuring device.
You have to divide the 8 litres of water equally between your two best friends, so that each gets 4 litres of water. How can you do this?
View the solution at Future Learn.
Day 30 | Going to St Ives
As I was going to St Ives
I met a man with seven wives.
Each wife had seven sacks,
Each sack had seven cats,
Each cat had seven kits;
Kits, cats, sacks, wives,
How many were going to St Ives?
Look at the solution to this well-known problem.
Day 31 | Alison’s quilt
Alison joins together nine squares with side lengths to form a rectangular quilt:
- 1cm
- 4cm
- 7cm
- 8cm
- 9cm
- 10cm
- 14cm
- 15cm
- 18cm
There are no gaps and no overlaps.
Can you find the dimensions of the finished quilt, and show how Alison fitted the squares together?
Take a look at this problem on NRICH.
Day 32 | Secret locker code
A man forgot the secret code to open his locker. But he remembers the following clues:
- Fifth number plus the third number equals fourteen
- First number is one less than twice the second number
- Fourth number is one more than the second number
- Second number plus the third number equals ten
- Sum of all five numbers is 30
Can you find out the secret code to help him out?
View the answer at DoRiddles.
Day 33 | Celebrity murder mystery

Ant and Dec couldn’t believe what they had discovered. The secret they had just learnt about a certain celebrity’s private life was unbelievable.
They confronted the celeb but were warned to keep their mouths shut. But the celebrity decided they couldn’t take any chances. Later that week, Ant and Dec were found poisoned in their dressing room.
When police arrived on the scene, they found 6 celebrities lurking around, but who is the guilty one? Your job is to find out who did it.
Download this KS3 algebra lesson activity and browse more algebra games.
Day 34 | Pairwise adding
Charlie chose five numbers: 2, 3, 4, 7, 10.
He added together pairs of numbers from his set, and got the following totals: 5, 7, 9, 10, 11, 12.
Can you find the totals that Charlie has missed?
Look at this problem on wild.maths.org.
Day 35 | Are they parallel?
Are the four vertical lines parallel, or not?
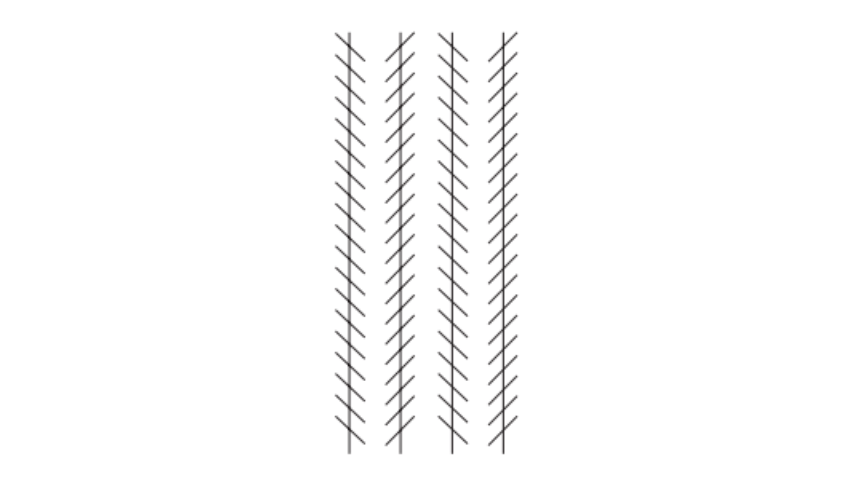
Find out the answer (and the reason behind it).
Day 36 | From town to town
The table below shows the distances (in miles) between a number of different towns
| A | B | C | D | E | F | |
| A | – | 10 | 13 | 12 | 15 | 20 |
| B | 10 | – | 8 | 7 | 11 | 5 |
| C | 13 | 8 | – | 6 | 9 | 14 |
| D | 12 | 7 | 6 | – | 18 | 2 |
| E | 15 | 11 | 9 | 18 | – | 3 |
| F | 20 | 5 | 14 | 2 | 3 | – |
Bob drives from Town A to Town E via Town D. He spends a total of 45 minutes driving to complete the journey.
Jane travels directly between two of the towns at exactly the same average speed as Bob.
Given that Jane’s journey took seven and a half minutes, find which two towns she drove between.
View the solution at M4ths.com.
Day 37 | Initial numbers maths puzzles
Each number has some initials after it. Work out what the initials mean – the numbers are clues. For example: 7 D in a W is 7 Days in a Week.
- 26 L in the A
- 7 C in the R
- 6 W of H the E
- 7 S on a F P P
- 1000 M in a K
- 64 S on a C B
- 1066 B of H
- 28 D in F
- 24 H in a D
- 8 L on a S
View more and see the answers at Math Sphere.
Day 38 | Midnight
If it were two hours later, it would be half as long until midnight as it would be if it were an hour later. What time is it now?
View the answer at BrainDen.
Day 39 | Aunt’s old jalopy
After visiting my Great Aunt Annie, I travelled home in her old jalopy. The car was old and battered. It had a leak from the petrol tank. I was stuck in second gear.
This meant that I could only travel along at a steady 30 miles per hour and managed a paltry 20 miles per gallon of fuel.
At the start of the journey I had placed exactly 10 gallons of fuel into the tank. I knew though, that the fuel tank lost fuel at the rate of half a gallon per hour.
Just as I arrived home, the car stopped because it had run out of fuel and I had only just made it.
How far was it from my Great Aunt’s to my home?
See the answer at Braingle.
Day 40 | Gift of gems
Four jewellers had respectively:
- 8 rubies
- 10 sapphires
- 100 pearls
- 5 diamonds
Each gave one gem from their collection to each of the rest.
Afterwards they noticed that they all had collections of gems of precisely equal value.
Can you work out the relative values of each gem?
Can you then work out how much each jeweller gained or lost?
This puzzle comes from NRICH.
Day 41 | The largest number
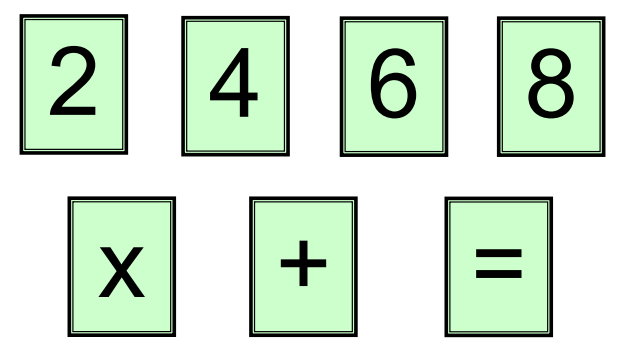
Using the numbers 2, 4, 6 and 8, the multiply sign, the add sign and the equals sign, what is the largest number you can make?
You may only press each digit and sign once, but you don’t have to press all the signs.
See the solution at Math Sphere.
Day 42 | Cross numbers maths puzzles

Across
3: 6 across plus 3
6: 7 across plus 6
7: 7 down plus 2
Down
1: 11 times 3 across
2: add digits of 5 down
4: 6 across plus 7 across
5: 9 times 7 across
7: two digits
Generate your own maths puzzles like this at Maths is Fun.
Browse more KS3 maths games and lesson ideas and GCSE maths games.


 (@PaulMathUn)
(@PaulMathUn)